Fullerene Structure and Bonding Index
- The Truncated Icosahedron
- Activity III.A
- Analysis of the Bonding in C
- Other Fullerenes
- Activity III.C
- Other Possible Structures for C
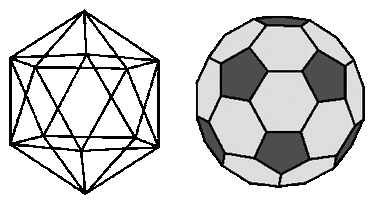
- The Truncated Icosahedron. The proposed structure for C, a "truncated icosahedron", is derived from an icosahedron by truncating or "snipping off" each of the twelve vertices (see Figure III.A). Hence, each vertex is replaced by a five-membered ring - a pentagon. This snipping process also converts each of the twenty former triangular faces into six-membered rings - hexagons.
Figure III.A:
Icosahedron (left) and "truncated icosahedron - Analysis of the Bonding in CIn the proposed structure for C, each vertex of the truncated icosahedron is occupied by a carbon atom, and each carbon is three-connected to other carbon atoms by one double bond and two single bonds. Carbon atoms with this kind of connectivity are usually referred to as "sp carbons" because the orbitals used to sigma-bond the three adjacent carbons are hybrids of the 2s orbital and the two 2p orbitals (2p and 2p). The remaining 2p orbital (2p) is responsible for the pi-bond.
Usually, an sp carbon and its three neighboring atoms are all coplanar. This is the case, for example, in graphite where there are infinite planar sheets of sp carbons arranged in edge-sharing hexagons. The p orbitals all lie parallel to each other and perpendicular to the graphite plane, generating a sea of - electron density above and below the plane.
In graphite, the C-C bonds are all equal in length and intermediate between normal single and double bonds. This "delocalization" can be explained by noting that graphite has many different but equivalent "resonance structures". (The resonance structures differ only in the placement of the double bonds.) Two of these are drawn for a portion of graphite in Fig. III.B.1. - Figure III.B.1:
- Two resonance structures of a portion of graphite. Clearly, the proposed structure for C is not planar! The angle between a p axis and a C-C bond vector, (see Figure III.B.2), is 101.6° (as compared to 90° in planar graphite) (Haddon, 1986, Vol. 131). The bowl-shape or concavity at each sp carbon center introduces some strain into the molecule. However, the high symmetry distributes that strain evenly across the entire structure.Figure III.B.2:
Theta () is defined as the angle between the p axis and a carbon-carbon bond vector. - Other Fullerenes. The truncated icosahedron is not the only possible fullerene-type structure. There are, in fact, many other hollow cage structures that can be constructed using only pentagons and hexagons (Kroto, 1987). Interestingly, each of these structures contains exactly twelve pentagons, while the number of hexagons is arbitrary. The pentagons are necessary for closure. (Recall that graphite, which consists only of fused hexagons, is essentially a planar sheet. While this sheet may warp and bend, it can never close.) The number of vertices in closed fullerene-type structures is necessarily even.
The smallest possible fullerene would be C, containing twelve pentagons and zero hexagons. However, such a structure would possess a great deal of strain, because the local topology at each carbon center would be highly non-planar. Other possible fullerenes include C, C, C, and C. Because the molecular strain tends to be concentrated in the five-membered rings that are responsible for closure, structures that avoid contiguous (edge-sharing) pentagons are particularly stable. It turns out that C and C are the smallest carbon clusters for which this can be achieved. - Other Possible Structures for C While the truncated icosahedron structure for C is elegant and aesthetically-pleasing, it is important to bear in mind that when it was proposed, there was only one piece of supporting experimental evidence - an unusually large peak at 720 in the mass spectrum. Other C cluster structures, including the following three, were possible.
- Planar graphite fragments.
The problem with this type of structure is that it contains many unsatisfied valences, and it is not clear why C should be any more stable than any other cluster size. - Cyclic polyalkynes.
In this structure, there are no unsatisfied valences but the stability of C vs. other cluster sizes is not easily rationalized. - Other fullerenes, i.e., other hollow cage structures with different atom arrangements.
These would necessarily be less highly symmetric than the truncated icosahedron and would less effectively distribute strain evenly around the molecule.
- Planar graphite fragments.